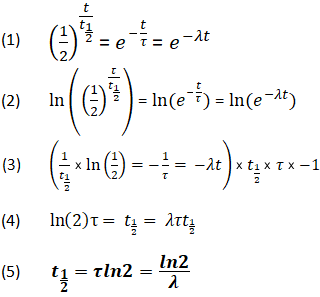Half-Life Calculator
The following tools can generate any one of the values from the other three in the half-life formula for a substance undergoing decay to decrease by half.
Half-Life Calculator
Result
quantity remains, Nt = 90.572366426391
Half-Life, Mean Lifetime, and Decay Constant Conversion
Please provide any one of the following to get the other two.
Definition and Formula
Half-life is defined as the amount of time it takes a given quantity to decrease to half of its initial value. The term is most commonly used in relation to atoms undergoing radioactive decay, but can be used to describe other types of decay, whether exponential or not. One of the most well-known applications of half-life is carbon-14 dating. The half-life of carbon-14 is approximately 5,730 years, and it can be reliably used to measure dates up to around 50,000 years ago. The process of carbon-14 dating was developed by William Libby, and is based on the fact that carbon-14 is constantly being made in the atmosphere. It is incorporated into plants through photosynthesis, and then into animals when they consume plants. The carbon-14 undergoes radioactive decay once the plant or animal dies, and measuring the amount of carbon-14 in a sample conveys information about when the plant or animal died.
Below are shown three equivalent formulas describing exponential decay:
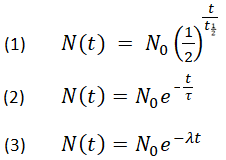
-
where
N0 is the initial quantity
Nt is the remaining quantity after time, t
t1/2 is the half-life
τ is the mean lifetime
λ is the decay constant
If an archaeologist found a fossil sample that contained 25% carbon-14 in comparison to a living sample, the time of the fossil sample's death could be determined by rearranging equation 1, since Nt, N0, and t1/2 are known.
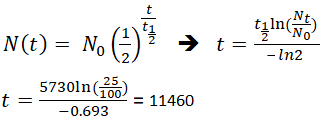
This means that the fossil is 11,460 years old.
Derivation of the Relationship Between Half-Life Constants
Using the above equations, it is also possible for a relationship to be derived between t1/2, τ, and λ. This relationship enables the determination of all values, as long as at least one is known.