Volume Calculator
The following is a list of volume calculators for several common shapes. Please fill in the corresponding fields and click the "Calculate" button.
Sphere Volume Calculator
 |
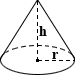
Cone Volume Calculator
 |
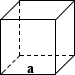
Cube Volume Calculator
 |
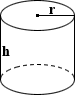
Cylinder Volume Calculator
 |
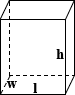
Rectangular Tank Volume Calculator
 |
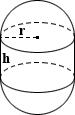
Capsule Volume Calculator
 |
Spherical Cap Volume Calculator
Please provide any two values below to calculate.
Conical Frustum Volume Calculator
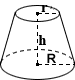 |
Ellipsoid Volume Calculator
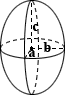 |
Square Pyramid Volume Calculator
 |
Tube Volume Calculator
 |
Volume is the quantification of the three-dimensional space a substance occupies. The SI unit for volume is the cubic meter, or m3. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces. Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method. Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes.
Sphere
A sphere is the three-dimensional counterpart of a two-dimensional circle. It is a perfectly round geometrical object that, mathematically, is the set of points that are equidistant from a given point at its center, where the distance between the center and any point on the sphere is the radius r. Likely the most commonly known spherical object is a perfectly round ball. Within mathematics, there is a distinction between a ball and a sphere, where a ball comprises the space bounded by a sphere. Regardless of this distinction, a ball and a sphere share the same radius, center, and diameter, and the calculation of their volumes is the same. As with a circle, the longest line segment that connects two points of a sphere through its center is called the diameter, d. The equation for calculating the volume of a sphere is provided below:
| volume = |
|
πr3 |
EX: Claire wants to fill a perfectly spherical water balloon with radius 0.15 ft with vinegar to use in the water balloon fight against her arch-nemesis Hilda this coming weekend. The volume of vinegar necessary can be calculated using the equation provided below:
volume = 4/3 × π × 0.153 = 0.141 ft3
Cone
A cone is a three-dimensional shape that tapers smoothly from its typically circular base to a common point called the apex (or vertex). Mathematically, a cone is formed similarly to a circle, by a set of line segments connected to a common center point, except that the center point is not included in the plane that contains the circle (or some other base). Only the case of a finite right circular cone is considered on this page. Cones comprised of half-lines, non-circular bases, etc. that extend infinitely will not be addressed. The equation for calculating the volume of a cone is as follows:
| volume = |
|
πr2h |
where r is the radius and h is the height of the cone
EX: Bea is determined to walk out of the ice cream store with her hard-earned $5 well spent. While she has a preference for regular sugar cones, the waffle cones are indisputably larger. She determines that she has a 15% preference for regular sugar cones over waffle cones and needs to determine whether the potential volume of the waffle cone is ≥ 15% more than that of the sugar cone. The volume of the waffle cone with a circular base with radius 1.5 in and height 5 in can be computed using the equation below:
volume = 1/3 × π × 1.52 × 5 = 11.781 in3
Bea also calculates the volume of the sugar cone and finds that the difference is < 15%, and decides to purchase a sugar cone. Now all she has to do is use her angelic, childlike appeal to manipulate the staff into emptying the containers of ice cream into her cone.
Cube
A cube is the three-dimensional analog of a square, and is an object bounded by six square faces, three of which meet at each of its vertices, and all of which are perpendicular to their respective adjacent faces. The cube is a special case of many classifications of shapes in geometry, including being a square parallelepiped, an equilateral cuboid, and a right rhombohedron. Below is the equation for calculating the volume of a cube:
volume = a3
where a is the edge length of the cube
EX: Bob, who was born in Wyoming (and has never left the state), recently visited his ancestral homeland of Nebraska. Overwhelmed by the magnificence of Nebraska and the environment unlike any other he had previously experienced, Bob knew that he had to bring some of Nebraska home with him. Bob has a cubic suitcase with edge lengths of 2 feet, and calculates the volume of soil that he can carry home with him as follows:
volume = 23 = 8 ft3
Cylinder
A cylinder in its simplest form is defined as the surface formed by points at a fixed distance from a given straight line axis. In common use, however, "cylinder" refers to a right circular cylinder, where the bases of the cylinder are circles connected through their centers by an axis perpendicular to the planes of its bases, with given height h and radius r. The equation for calculating the volume of a cylinder is shown below:
volume = πr2h
where r is the radius and h is the height of the tank
EX: Caelum wants to build a sandcastle in the living room of his house. Because he is a firm advocate of recycling, he has recovered three cylindrical barrels from an illegal dumping site and has cleaned the chemical waste from the barrels using dishwashing detergent and water. The barrels each have a radius of 3 ft and a height of 4 ft, and Caelum determines the volume of sand that each can hold using the equation below:
volume = π × 32 × 4 = 113.097 ft3
He successfully builds a sandcastle in his house, and as an added bonus, manages to save electricity on nighttime lighting, since his sandcastle glows bright green in the dark.
Rectangular Tank
A rectangular tank is a generalized form of a cube, where the sides can have varying lengths. It is bounded by six faces, three of which meet at its vertices, and all of which are perpendicular to their respective adjacent faces. The equation for calculating the volume of a rectangle is shown below:
volume= length × width × height
EX: Darby likes cake. She goes to the gym for 4 hours a day, every day, to compensate for her love of cake. She plans to hike the Kalalau Trail in Kauai and though extremely fit, Darby worries about her ability to complete the trail due to her lack of cake. She decides to pack only the essentials and wants to stuff her perfectly rectangular pack of length, width, and height 4 ft, 3 ft and 2 ft respectively, with cake. The exact volume of cake she can fit into her pack is calculated below:
volume = 2 × 3 × 4 = 24 ft3
Capsule
A capsule is a three-dimensional geometric shape comprised of a cylinder and two hemispherical ends, where a hemisphere is half a sphere. It follows that the volume of a capsule can be calculated by combining the volume equations for a sphere and a right circular cylinder:
| volume = πr2h + |
|
πr3 = πr2( |
|
r + h) |
where r is the radius and h is the height of the cylindrical portion
EX: Given a capsule with a radius of 1.5 ft and a height of 3 ft, determine the volume of melted milk chocolate m&m's that Joe can carry in the time capsule he wants to bury for future generations on his journey of self-discovery through the Himalayas:
volume = π × 1.52 × 3 + 4/3 ×π ×1.53 = 35.343 ft3
Spherical Cap
A spherical cap is a portion of a sphere that is separated from the rest of the sphere by a plane. If the plane passes through the center of the sphere, the spherical cap is referred to as a hemisphere. Other distinctions exist, including a spherical segment, where a sphere is segmented with two parallel planes and two different radii where the planes pass through the sphere. The equation for calculating the volume of a spherical cap is derived from that of a spherical segment, where the second radius is 0. In reference to the spherical cap shown in the calculator:
| volume = |
|
πh2(3R - h) |
Given two values, the calculator provided computes the third value and the volume. The equations for converting between the height and the radii are shown below:
Given r and R: h = R ± √R2 - r2
| Given r and h: R = |
|
where r is the radius of the base, R is the radius of the sphere, and h is the height of the spherical cap
EX: Jack really wants to beat his friend James in a game of golf to impress Jill, and rather than practicing, he decides to sabotage James' golf ball. He cuts off a perfect spherical cap from the top of James' golf ball, and needs to calculate the volume of the material necessary to replace the spherical cap and skew the weight of James' golf ball. Given James' golf ball has a radius of 1.68 inches, and the height of the spherical cap that Jack cut off is 0.3 inches, the volume can be calculated as follows:
volume = 1/3 × π × 0.32 (3 × 1.68 - 0.3) = 0.447 in3
Unfortunately for Jack, James happened to receive a new shipment of balls the day before their game, and all of Jack's efforts were in vain.
Conical Frustum
A conical frustum is the portion of a solid that remains when a cone is cut by two parallel planes. This calculator calculates the volume for a right circular cone specifically. Typical conical frustums found in everyday life include lampshades, buckets, and some drinking glasses. The volume of a right conical frustum is calculated using the following equation:
| volume = |
|
πh(r2 + rR + R2) |
where r and R are the radii of the bases, h is the height of the frustum
EX: Bea has successfully acquired some ice cream in a sugar cone, and has just eaten it in a way that leaves the ice cream packed within the cone, and the ice cream surface level and parallel to the plane of the cone's opening. She is about to start eating her cone and the remaining ice cream when her brother grabs her cone and bites off a section of the bottom of her cone that is perfectly parallel to the previously sole opening. Bea is now left with a right conical frustum leaking ice cream, and has to calculate the volume of ice cream she must quickly consume given a frustum height of 4 inches, with radii 1.5 inches and 0.2 inches:
volume=1/3 × π × 4(0.22 + 0.2 × 1.5 + 1.52) = 10.849 in3
Ellipsoid
An ellipsoid is the three-dimensional counterpart of an ellipse, and is a surface that can be described as the deformation of a sphere through scaling of directional elements. The center of an ellipsoid is the point at which three pairwise perpendicular axes of symmetry intersect, and the line segments delimiting these axes of symmetry are called the principal axes. If all three have different lengths, the ellipsoid is commonly described as tri-axial. The equation for calculating the volume of an ellipsoid is as follows:
| volume = |
|
πabc |
where a, b, and c are the lengths of the axes
EX: Xabat only likes eating meat, but his mother insists that he consumes too much, and only allows him to eat as much meat as he can fit within an ellipsoid shaped bun. As such, Xabat hollows out the bun to maximize the volume of meat that he can fit in his sandwich. Given that his bun has axis lengths of 1.5 inches, 2 inches, and 5 inches, Xabat calculates the volume of meat he can fit in each hollowed bun as follows:
volume = 4/3 × π × 1.5 × 2 × 5 = 62.832 in3
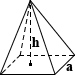
Square Pyramid
A pyramid in geometry is a three-dimensional solid formed by connecting a polygonal base to a point called its apex, where a polygon is a shape in a plane bounded by a finite number of straight line segments. There are many possible polygonal bases for a pyramid, but a square pyramid is a pyramid in which the base is a square. Another distinction involving pyramids involves the location of the apex. A right pyramid has an apex that is directly above the centroid of its base. Regardless of where the apex of the pyramid is, as long as its height is measured as the perpendicular distance from the plane containing the base to its apex, the volume of the pyramid can be written as:
Generalized pyramid volume:
| volume = |
|
bh |
Square pyramid volume:
| volume = |
|
a2h |
EX: Wan is fascinated by ancient Egypt and particularly enjoys anything related to the pyramids. Being the eldest of his siblings Too, Tree and Fore, he is able to easily corral and deploy them at his will. Taking advantage of this, Wan decides to re-enact ancient Egyptian times and have his siblings act as workers building him a pyramid of mud with edge length 5 feet and height 12 feet, the volume of which can be calculated using the equation for a square pyramid:
volume = 1/3 × 52 × 12 = 100 ft3
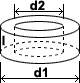
Tube Pyramid
A tube, often also referred to as a pipe, is a hollow cylinder that is often used to transfer fluids or gas. Calculating the volume of a tube essentially involves the same formula as a cylinder (volume=pr2h), except that in this case, the diameter is used rather than the radius, and length is used rather than height. The formula, therefore, involves measuring the diameters of the inner and outer cylinder, as shown in the figure above, calculating each of their volumes, and subtracting the volume of the inner cylinder from that of the outer one. Considering the use of length and diameter mentioned above, the formula for calculating the volume of a tube is shown below:
| volume = π |
|
l |
where d1 is the outer diameter, d2 is the inner diameter, and l is the length of the tube
EX: Beulah is dedicated to environmental conservation. Her construction company uses only the most environmentally friendly of materials. She also prides herself on meeting customer needs. One of her customers has a vacation home built in the woods, across a creek. He wants easier access to his house, and requests that Beulah build him a road, while ensuring that the creek can flow freely so as not to disrupt his favorite fishing spot. She decides that the pesky beaver dams would be a good point to build a pipe through the creek. The volume of patented low-impact concrete required to build a pipe of outer diameter 3 feet, inner diameter 2.5 feet, and length of 10 feet, can be calculated as follows:
| volume = π × |
|
× l0 = 21.6 ft3 |
Common Volume Units
| Unit | cubic meters | milliliters |
| milliliter (cubic centimeter) | 0.000001 | 1 |
| cubic inch | 0.00001639 | 16.39 |
| pint | 0.000473 | 473 |
| quart | 0.000946 | 946 |
| liter | 0.001 | 1,000 |
| gallon | 0.003785 | 3,785 |
| cubic foot | 0.028317 | 28,317 |
| cubic yard | 0.764555 | 764,555 |
| cubic meter | 1 | 1,000,000 |
| cubic kilometer | 1,000,000,000 | 1015 |