Surface Area Calculator
Use the calculators below to calculate the surface area of several common shapes.
Ball Surface Area
 |
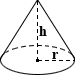
Cone Surface Area
 |
Cube Surface Area
 |
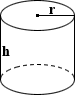
Cylindrical Tank Surface Area
 |
Rectangular Tank Surface Area
 |
Capsule Surface Area
 |
Cap Surface Area
Please provide any two values below to calculate.
Conical Frustum Surface Area
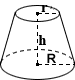 |
Ellipsoid Surface Area
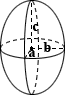 |
Square Pyramid Surface Area
 |
The surface area of a solid is a measure of the total area occupied by the surface of an object. All of the objects addressed in this calculator are described in more detail on the Volume Calculator and Area Calculator pages. As such, this calculator will focus on the equations for calculating the surface area of the objects and the use of these equations. Please refer to the aforementioned calculators for more detail on each individual object.
Sphere
The surface area (SA) of a sphere can be calculated using the equation:
SA = 4πr2
where r is the radius
Xael doesn't like sharing her chocolate truffles with anyone. When she receives a box of Lindt truffles, she proceeds to calculate the surface area of each truffle in order to determine the total surface area she has to lick to decrease the probability that anyone will try to eat her truffles. Given that each truffle has a radius of 0.325 inches:
SA = 4 × π × 0.3252 = 1.327 in2
Cone
The surface area of a circular cone can be calculated by summing the surface area of each of its individual components. The "base SA" refers to the circle that comprises the base in a closed circular cone, while the lateral SA refers to the rest of the area of the cone between the base and its apex. The equations to calculate each, as well as the total SA of a closed circular cone are shown below:
base SA = πr2
lateral SA = πr√r2 + h2
total SA = πr(r + √r2 + h2)
where r is the radius and h is the height
Athena has recently taken an interest in Southeast Asian culture, and is particularly fascinated by the conical hat, typically referred to as a "rice hat," which is commonly used in a number of southeast Asian countries. She decides to make one of her own, and being a very practical person not mired in sentimentality, retrieves her mother's wedding dress from the dark recesses of the wardrobe in which it resides. She determines the surface area of material she needs to create her hat with a radius of 1 foot and a height of 0.5 feet as follows:
lateral SA = π × 0.4√0.42 + 0.52 = 0.805 ft2
Cube
The surface area of a cube can be calculated by summing the total areas of its six square faces:
SA = 6a2
where a is the edge length
Anne wants to give her younger brother a Rubik's cube for his birthday, but knows that her brother has a short attention span and is easily frustrated. She custom orders a Rubik's Cube in which all the faces are black, and has to pay for the customization based on the surface area of the cube with an edge length of 4 inches.
SA = 6 × 42 = 96 in2
Cylindrical Tank
The surface area of a closed cylinder can be calculated by summing the total areas of its base and lateral surface:
base SA = 2πr2
lateral SA = 2πrh
total SA = 2πr(r + h)
where r is the radius and h is the height
Jeremy has a large cylindrical fish tank that he bathes in because he doesn't like showers or bathtubs. He is curious whether his heated water cools faster than when in a bathtub, and needs to calculate the surface area of his cylindrical tank of height 5.5 feet and radius of 3.5 feet.
total SA = 2π × 3.5(3.5 + 5.5) = 197.920 ft2
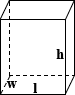
Rectangular Tank
The surface area of a rectangular tank is the sum of the area of each of its faces:
SA = 2lw + 2lh + 2wh
where l is the length, w is the width, and h is the height
Banana, the eldest daughter of a long line of banana farmers, wants to teach her spoiled rotten little sister, Banana-Bread, a lesson about hope and expectations. Banana-Bread has been clamoring all week long about wanting a new set of drawers to house her new Batman action figures. As such, Banana buys her a large Barbie doll house with limited edition kitchen utensils, oven, apron, and realistic rotting bananas for Batman. She packs these into a rectangular box of similar dimensions as the drawer that Banana-Bread wants, and needs to determine the amount of wrapping paper she needs to complete her presentation of the gift of the 3 ft × 4 ft × 5 ft surprise:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 ft2
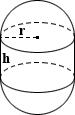
Capsule
The surface area of a capsule can be determined by combining the surface area equations for a sphere and the lateral surface area of a cylinder. Note that the surface area of the bases of the cylinder is not included since it does not comprise part of the surface area of a capsule. The total surface area is calculated as follows:
SA = 4πr2 + 2πrh
where r is the radius and h is the height
Horatio is manufacturing a placebo that purports to hone a person's individuality, critical thinking, and ability to objectively and logically approach different situations. He has already tested the market and has found that a vast majority of the sample population exhibit none of these qualities, and are very ready to purchase his product, further entrenching themselves within the traits they so desperately seek to escape. Horatio needs to determine the surface area of each capsule so that he can coat them with an excessive layer of sugar and appeal to the sugar predisposed tongues of the population in preparation for his next placebo that "cures" all forms of diabetes mellitus. Given each capsule has r of 0.05 inches and h of 0.5 inches:
SA = 4π × 0.052 + 2π × 0.05 × 0.5 = 0.188 in2
Spherical Cap
The surface area of a spherical cap is based on the height of the segment in question. The calculator provided assumes a solid sphere and includes the base of the cap in the calculation of surface area, where the total surface area is the sum of the area of the base and that of the lateral surface of the spherical cap. If using this calculator to compute the surface area of a hollow sphere, subtract the surface area of the base. Given two values of height, cap radius, or base radius, the third value can be calculated using the equations provided on the Volume Calculator. The surface area equations are as follows:
spherical cap SA = 2πRh
base SA = πr2
Total solid sphere SA = 2πRh + πr2
where R is the spherical cap radius, r is the base radius, and h is the height
Jennifer is jealous of the globe that her older brother Lawrence received for his birthday. Since Jennifer is two-thirds the age of her brother, she decides that she deserves one-third of her brother's globe. After returning her father's hand saw to the toolshed, she calculates the surface area of her hollow portion of the globe with R of 0.80 feet and h 0.53 feet as shown below:
SA = 2π × 0.80 × 0.53 = 2.664 ft2
Conical Frustum
The surface area of a solid, right conical frustum is the sum of the areas of its two circular ends and that of its lateral face:
circular end SA = π(R2 + r2)
lateral SA = π(R+r)√(R-r)2 + h2
total SA = π(R2 + r2) + π(R+r)√(R-r)2 + h2
where R and r are the radii of the ends, h is the height
Paul is making a volcano in the shape of a conical frustum for his science fair project. Paul views volcanic eruptions as a violent phenomenon, and being against all forms of violence, decides to make his volcano in the form of a closed conical frustum that does not erupt. Although his volcano is unlikely to impress the science fair judges, Paul must still determine the surface area of material he needs to coat the outer wall of his volcano with R of 1 foot, r of 0.3 feet, and h of 1.5 feet:
total SA = π(12 + 0.32) + π(1 + 0.3) √(1 - 0.3)2 + 1.52 = 10.185 ft2
Ellipsoid
Calculating the surface area of an ellipsoid does not have a simple, exact formula such as a cube or other simpler shape does. The calculator above uses an approximate formula that assumes a nearly spherical ellipsoid:
SA ≈ 4π 1.6√(a1.6b1.6 + a1.6c1.6 + b1.6c1.6)/3
where a, b, and c are the axes of the ellipse
Coltaine has always enjoyed cooking and recently won a ceramic knife from a contest. Unfortunately for his family, who almost exclusively eat meat, Coltaine has been practicing his cutting technique on an excessive amount of vegetables. Rather than eating his vegetables, Coltaine's father stares dejectedly at his plate, and estimates the surface area of the elliptical cuts of zucchini with axes 0.1, 0.2, and 0.35 inches:
SA ≈ 4π 1.6√(0.11.60.21.6 + 0.11.60.351.6 + 0.21.60.351.6)/3 = 0.562 in2
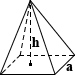
Square Pyramid
The surface area of a square pyramid is comprised of the area of its square base and the area of each of its four triangular faces. Given height h and edge length a, the surface area can be calculated using the following equations:
base SA = a2
lateral SA = 2a√(a/2)2 + h2
total SA = a2 + 2a√(a/2)2 + h2
Vonquayla's classroom recently completed building a model of the Great Pyramid of Giza. However, she feels that the model does not exude the feeling of architectural wonder that the original does and decides that coating it with "snow" would at least impart an aspect of wonder. She calculates the surface area of melted sugar she would need to fully coat the pyramid with edge length a of 3 feet and height h of 5 feet:
total SA = 32 + 2 × 3√(3/2)2 + 52 = 40.321 ft2
Unlike the Great Pyramid of Giza that has stood for thousands of years, its model, made of graham crackers and coated in sugar, lasted only a matter of days.
Common Area Units
| Unit | meter2 |
| kilometer2 | 1,000,000 |
| centimeter2 | 0.0001 |
| millimeter2 | 0.000001 |
| micrometer2 | 0.000000000001 |
| hectare | 10,000 |
| mile2 | 2,589,990 |
| yard2 | 0.83613 |
| foot2 | 0.092903 |
| inch2 | 0.00064516 |
| acre | 4,046.86 |