Statistics Calculator

or Provide Values Separated by Comma Below

Above is a simple, generalized statistics calculator that computes statistical values such as the mean, population standard deviation, sample standard deviation, and geometric mean among others. Many of these values are more well described in other calculators also available on this website. Visit the hyperlinks provided for more detail on how to calculate these values, as well as basic examples and applications of each. Note that while the computation of variance is not explicitly shown, it is calculated as the standard deviation squared, or σ². Simply ensure that the correct standard deviation is being used (s vs. σ) and square the value to obtain the variance.

Geometric Mean

The geometric mean in mathematics is a type of average that uses the product of the values in a set to indicate central tendency. This is in contrast to the arithmetic mean that performs the same function using the sum of the values in the set rather than their products. The geometric mean is useful in cases where the values being compared vary largely. Imagine a car that is rated on a scale of 0-5 for fuel efficiency, and a scale of 0-100 for safety. If the arithmetic means were used, the safety of the vehicle would be given far more weight, since a small percentage change on a larger scale will result in a larger difference than a large percentage change on a smaller scale; a change of fuel efficiency rating from 2 to 5 which is a 250% increase in rating would be overshadowed by a 6.25% rating change of 80 to 85 if only the arithmetic mean were considered. The geometric mean accounts for this by normalizing the ranges being averaged, resulting in none of the ranges dominating the weighting. Unlike the arithmetic mean, any given percentage change in the geometric mean has the same effect on the geometric mean. The equation for calculating the geometric mean is as follows:

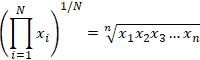
In the equation above, i is the index that refers to the location of a value in a set, x_i is an individual value, and N is the total number of values. i=1 refers to the starting index, i.e. for a data set 1, 5, 7, 9, 12, i=1 is 1, i=2 is 5, i=3 is 7, and so on. The notation above essentially means to multiply each value in the set through the n^th value, and then take the n^th root of the product. Refer to the root calculator if necessary for a review of n^th roots. Below is an example using the listed data set:

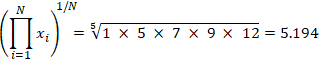
The geometric mean has applications within proportional growth, the social sciences, aspect ratios, geometry, and finance among others, and like most other statistical values, can provide highly useful information when used in the proper contexts.